python PIL 图片处理库
最近学习了 python 的图形处理库 PIL,深刻体会到 python 的强大。就图片的简单处理,如高亮、旋转、resize 等操作,特别是对图片的批量处理,python 较 photoshop 等图片处理工具要来的更容易、更方便。
安装 PIL 库后,根据自己的需求阅读 PIL 库的使用手册。下面是我在使用该 lib 时,遇到的一些问题和感悟。
需求:在图片右上方添加如手机 App 上消息提醒的数字。
具体实现代码如下:
#!/usr/bin/python
import os, sys
from PIL import Image
from PIL import ImageFont
from PIL import ImageDraw
def main():
img = Image.open("thumb.png")
fontsize = img.size[1] / 16
x = img.size[0] - fontsize
draw = ImageDraw.Draw(img)
font = ImageFont.truetype("/usr/share/fonts/truetype/msttcorefonts/arial.ttf", fontsize)
draw.text((x, 0), "9", font=font, fill="red")
del draw
img.save("result.png")
img.show()
if __name__== '__main__':
main()
分析:
1. 坐标 (0, 0) 表示左上角,整个图片类似镶嵌在坐标的第四像限;img.size 是一个二位数组,依次位图片的宽和高。
2. 在图片上添加内容时注意对应内容也会占位置,所以不能当作点即 pixel 来看待,实际处理时需要考虑添加对象的 size,这就对应代码中右上角坐标 x 的获取。
3. ImageFont 的获取有很多方法,其中较简单的方法从 truetype 中获取,对应 font 存放的位置一般是 /usr/share/fonts/...
摘录
有时候觉得有些话、有些内容挺让人受启发的,这种启发是各方面的,其影响甚至可以受用一生。当我们烦躁不安时,静心品读,或许生命又会被着上别样的色彩。集中做一下摘录如下:
1. 如同分析代码,只看输出的总体时间是难以优化的,关键是整个过程的不同阶段的耗时(注意二八定律);
2. 金融的本质是永远用你的钱,为比你更有钱的人服务。
索罗斯投资理念是:量子最基本的特征是无论怎么改变实验方式、观察技术,都不可能改变量子轨迹的不确定性。
——《世界是一部金融史》
3. 这些年,我发现学历跟人生快不快乐没有什么关系,重点是一个人的生活态度:能不能幽默的看待自己以及这个世界。
阿拓总能用十年后的心态来看待眼前的事物,这就是为什么他好脾气的原因。如果你每一次遇到事情都能跳出来,用一种更成熟的眼光来审视,可能很多事情都会豁达很多。
——《等一个人咖啡》
4.人与人的差别就是习惯的差别:如果一时间作为坐标横轴,每天的习惯好坏按分支高低作为纵轴,对时间轴进行积分的话,最终的面积结果就是一个人一生的成就总量,你会发现,和他人一丢丢的习惯上的微小差距,在岁月的作用下,成就的面积差距是如此的巨大。因此,任何一个有非凡成就的人,从外界看,可能会有很多机缘,但从内功来看,这些习惯一定是不可或缺的,并非偶然。
(未完待续)
Ubuntu 右上角小键盘不见了解决方法
好久没用电脑了,打开电脑,发现发现输入法不能切换且 ubuntu 右上角的小键盘不见了,再网上搜索方法如下:
打开终端,在终端里输入如下命令:
1. killall ibus-daemon
2. ibus-daemon -d
ibus 输入法偶尔会挂掉,结束进程,再重新启动即可。
那片梧桐
蓊郁的交织
织出片片阳光的细碎
那片梧桐
曳落点点路面的斑驳
啊 那片梧桐
倒映在春日里的 是
舞散着的 满天精灵
虽
眯了眼 搔了鼻 催了泪
却
顽皮着新生的预告
啊 那片梧桐
怒放在夏日里的 是
最惬意的阴凉
步伐的闲适
细语的淙淙
漾出阵阵 人与自然
悠远的祥和
啊 那片梧桐
弹奏在秋日里的 是
生命的真实
没有喧嚣
没有热烈
夜夜细雨唤醒了
迟暮的枯黄
空气里 飘荡起
缕缕叶落归根的轨迹
啊 那片梧桐
吟诵在冬日里的 是
漫漫等待的坚忍
寒风
肆意创作着自己的泼墨画
条条枝桠
裁剪出朵朵透明的晶莹
黑白的交替
融化了那份冗长的孤寂
啊
那片梧桐
一位研究生的学习感悟——采撷篇
由于现实世界太过于复杂而且充满不确定性,远非有限的生命用经验能够理解,因此先哲们基于一系列假设把现实世界简化到从概率上来说正确,从复杂程度上来说可认知的程度,就得到了知识(理论)。正因为简化,所以知识是不完全的,即使对同样一个事件,由于观察角度不同,简化标准不一,都可以得到不同的理论,但是这些理论都是“对”的,但也是不全面的;只有“观察——简化——推理——判断”的“活”的思维习惯才能帮助人相对正确的简化现实世界,超越表象,在理论上做出创新,在实践中高瞻远瞩。(把握好不确定性,使得理想与现实的矛盾得以调和)
————有时候,我们去解读一个人或者一件事情时,往往也是片面的去下定论,殊不知,或许我们看到只是片面,只是表象。有时候,选择沉默,选择用心去深入看,可能是最明智的做法。
在学校里,“横扫图书馆”的生活并不属于我,因为这既不可能,也不可以。虽然每个领域都如此的吸引人去思考,每一套理论体系都能解释很多的现象,但是没有一个理论能解释和语言所有的现象,没有一个理论能消除未来的不确定性。
很诧异这世界上优秀的人怎么会用同样的时间融合那么多的知识?
其实,他们不是看了那么多文献才提出自己的见解的,对每一个现象都是先自己观察,自己思考,理清其中的逻辑脉络,形成自己的观点再去看别人的文献,这样你可以知道每个人的贡献在何处,缺陷在何处,你会发现事实上很多文章是不值得看的,活的思维远比死的理论重要。(放弃“博而不专”的习惯吧,不要以“真实有用”作为评价理论的标准,注重培养自己的思维,分析理论观察什么,简化了什么,如何推理。要求自己去思考而不是记忆)
教育的目的不是学习知识,也没有任何知识可以在复杂多变的真实世界中给出确定的答案,可以让人不加思考的执行就获得幸福。教育的目的只在于培养人面对不确定性的能力,使人形成自己习惯的思维方式,懂得如何去观察这个世界复杂的现象,对其进行简化,提取重要的信息分析、综合,然后做出推理、判断,最后依据事实反思、修正自己思维的过程。
现实不但要求我们简化纷繁额表象,也要求我们把那些理论简化了的东西还原回去。
虽然思维比理论更加重要,但这并不意味着我们可以不学习理论而自由的放纵思想;恰恰相反,要获得思维,理论是最好的训练。(研究生阶段学习应该分为三个阶段:掌握基本工具,掌握思维方式并熟悉一个领域,用规范的方法表达新的观点)
————我们在学习知识时,不要只想着去接收,而是要站在他人的肩膀上,对理论有所贡献。就如读论文,我们想到的不应该知识吸收、赞同是它所表达的内容,而是在把握整体框架的基础上,思考为什么作者会这样做,这样去解决问题,得到的结果又是什么?当然最后更重要的也是思考作者在解决问题上还有没有缺陷。
“理论只是一张地图而不是现实的路径”。我们不用在“真实性”上做任何纠缠,我们也不需要精确的描绘每一方面而只需要抽象出轮廓,这在这个复杂的世界中已经足够了。所谓的简化,是指用尽可能少的变量解释尽可能多的现象,不但在空间上稳定,而且要在时间上能够承受历史的考验,这样才能最大限度的节约信息。理论的正确性不在于能 $100\%$ 预测未来。
理论绝不是枯燥的,高深的数学相对于现实是一种简化,一部部巨著,一首首诗篇、一部部电影、一幕幕舞蹈、一曲曲音乐相对于这个世界如何不是一种简化?
————停下匆忙的脚步吧,给大脑一点自由发挥的空间,其实眼前的万物都可以被思维,被简化,被抽象。
对问题进行分析和评论,写作能强迫你认真的分析,加深对现实的理解。
Galois 域上运算实现与优化归纳
此文主要就 Galois 域上的运算方法及其优化进行归纳总结:
Galois 域及运算在很多领域都有很好的应用,特别是信息的加解密、数字签名、存储系统的编码等。所以底层 Galois 域运算的效率至关重要。Galois 域内的运算有加减乘除四种,而乘除所花费的代价是最多的,所以针对 Galois 域上运算的优化主要是针对乘除来说的。
方法一:基于 log/antilog tables 的 look-up tables (上一篇文章有所论述):

方法二:full-multiplication table (full look-up table):
log/antilog tables 这种方法中用到了三次查表操作,基于此较好的优化方法是将有限域内所有元素的乘积都存储在表格中,即 full look-up table,此时之需要一次查表操作即可完成。但是此方法有一个明显的缺陷:针对 $w$ 较小的情况是可行的,但是当其增大时,表格所需的存储空间也会以指数形式增大,当 $w = 8$ 时,需要 64KB,当 $w = 16$ 时,需要的空间为 8GB,目前位置的计算机内存空间显然满足不了要求。
方法三:针对 log/antilog tables 的优化:
标准的 log/antilog tables 算法只要两个检验 $0$ 分支,三个查表操作,一个加法和取模操作。基于此,Huang 和 Xu 提出了三种优化方法:
1. 通过元素移位替代取模操作,如下(首先仍要判断是否为 $0$)
$$antilog[(log[a] + log[b]) & (2^n - 1) + (log[a] + log[b]) >> n]$$
2. 通过扩大 antilog table 替代取模操作,具体就是将该 table 扩展到 $-2^l + 1$ 到 $2^l - 2$,进而直接查表即可(首先仍要判断是否为 $0$)。
$$a * b = antilog[log[a] + log[b]]$$
3. 取消是否为 $0$ 的分支判断,和 Broder 的方法一样:
要取消分支判断,可以通过进一步扩大 antilog table,使元素 $0$ 在运算时得到映射。假设令 $logf[0] = 2Q$ (其中 $Q = 2^w$),则进行如下操作:
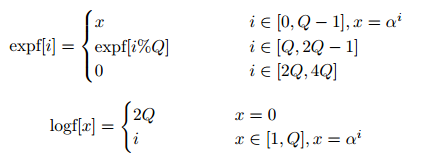
最后对应的代码是:

方法四:double tables or left-right table:
该中方法主要是针对 full multiplication table 而言的优化,原者的缺点是在 $w$ 较大的情况下,现有内存满足不了要求,故此方法就是退而将空间减小。两个元素 $a(x) = a_1 + a_{2}x + ... + a_{l - 1}x^{l - 1}$ 和 $b(x) = b_1 + b_{2}x + ... + b_{l - 1}x^{l - 1}$ 属于 $GF(2^l)$,则将两者相成具体可以表示为:
$$a(x) * b(x)
= (a_1 + ... + a_{l - 1}x^{l - 1}) * (b_1 + ... + b_{l - 1}x^{l - 1})
= ((a_1 + ... + a_{\frac{l}{2} - 1}x^{\frac{l}{2} - 1}) *
(b_1 + ... + b_{l - 1}x^{l - 1})) + ((a_{\frac{l}{2}}x^{\frac{l}{2}}
+ ... + a_{l - 1}x^{l - 1}) * (b_1 + ... + b_{l - 1}x^{l - 1}))$$
这样优化可将原来需求的 $2^l * 2^l$ 空间减小到 $2^l * 2^{\frac{l}{2}}$。对应的实现可以表示成如下:

方法五:使用 composite fields:
如其名,该方法主要是将运算的基底改变,基于较小的域来实现较大域的运算。即 $GF(2^n) = GF((2^l)^k)$,其中 $n = l * k$。进一步我们可以称 $GF(2^n)$ 是基于 $GF(2^l)$ 、度为 $k - 1$ 的多项式的集合。根据有限域运算的规则,现在的问题是需要找到一个基于 $GF(2^l)$ 的度数为 $k$ 的本源多项式 $f(x)$,现有的 Ben-Or 算法是一个比较有效的寻找本源多项式的算法,以 $GF((2^l)^2)$ 为例说明:
此时得到的本源多项式为 $f(x) = x^2 + s*x + 1$,该域中的两个元素 $a_1x + a_0$ 和 $b_1x + b_0$,两者相成可以表示成:
$$(a_1x + a_0) * (b_1x + b_0) = a_1b_1x^2 + (a_1b_0 + a_0b_1)x + a_0b_0$$
根据本源多项式有 $x^2 = sx + 1$ mod $f(x)$,则上式可以表示成
$$(a_1b_0 + a_0b_1 + sa_1b_1)x + (a_1b_1 + a_0b_0)$$
所以在 $GF((2^l)^2)$ 上的乘法运算主要是基于 $GF(2^l)$ 的五个乘法运算。此时空间得到了大量节省,但是需要计算额外的多个乘法,特别是当域增大时,乘法数量可能还会增加,这样到最后得到的性能可能会有所降低。
在 composite fields 上的求反运算最快的方法是使用 Extended Euclidean Algorithm。
(PS:在加解密中,域的大小会影响安全度,所以对大域的研究主要集中在这个应用中)
方法六:2-D table look-up:
这算是一种比较自然的想法,将乘法结果和除法结果都分别放置到二维表格中,具体计算时直接查表即可。
最后还要提一下很多论文中都会出现的一个表格:
| Space | Complexity | |
| Mult. Table | $2^l * 2^l$ | 1 LKU |
| Lg/Antilg | $2^l + 2^l$ | 3 LKU, 2 BR, 1MOD, 1 ADD |
| Lg/Antilg Optimized | $5 * 2^l$ | 3 LKU, 1 ADD |
| Huang and Xu | $2^l + 2^l$ | 3 LKU, 1 BR, 3 ADD, 1 SHIFT, 1 AND |
|
LR Mult. Table |
$2^{\frac{3l}{2} + 1}$ | 2 LKU, 2 AND, 1 XOR, 1 SHIFT |
内存分配方法及字符(串)操作小结
一. 内存分配方法
内存分配方法在不同的语言下有不同的方法,但是原理都大同小异。下面主要就 C 和 C++ 中的内存分配方法做分析。
C 中的内存分配方法主要有 malloc/free 和 memset 这两种。malloc/free 也是动态申请内存和释放内存,具体使用很简单:
int **a; a = (int **) malloc(m * sizeof(int *)); free(a);
而 memset 函数是在 C 语言的头文件 string.h 中包含的。需要谨慎使用这个函数,因为其是以字节为单位进行赋值(在 int 等类型是使用该函数时需要注意)的,同时在内存的连续性问题上也有一定的相关性。函数原型如下,其中指针p为所操作的内存空间的首地址,c为每个字节所赋的值,n为所操作内存空间的字节长度,也就是内存被赋值为c的字节数。(memset 更多使用在 bool 类型的赋值中)
void * memset (void * p,int c,size_t n);
C++ 中内存分配的方法主要是 new/delete。其中 new 调用构造函数完成动态分配和初始化工作,而 delete 会调用对象的析构函数,清理和释放掉内存。delete 有两种用法,对于内建简单数据类型,delete 和 delete [] 的功能是相同的。对于自定义的复杂数据类型,delete 和 delete [] 就不能互用,简单说来,前者是删除一个指针,后者是删除一个数组。注意 new 和 delete 不是函数,而是 C++ 的运算符。具体使用如:
int a[10]; a = new int[10];//new int(7), namely the initial value is 7; delete a; // or delete []a;
二. 字符(串)操作
算法中常常会有字符(串)等的操作。需要注意的是字符(串)和其他基本类型如 int 型等操作有很大不同,特别是四则运算上,‘0’ 和 0 也有区别。。。
C 语言处理主要几个函数有 strcpy(), strcat(), strcmp(), strlen() 等,比较死板,但是速度却很快。
python 在处理字符(串)时,个人觉得还是比较不错的,代码简洁,但是却会有大量时间的代价。(之前对同一字符(串)操作分别用 c 和 python 写了两段代码,运行的结果是后者时间是前者的 4 倍)
C++ 中可以使用 C 的字符(串)操作方法,包含头文件是 cstring.h。而 C++ 本身有一个 string.h 的库,也算是一个类(感觉几乎所有的 C 的方法都可以看作是一个类)。标准C++中提供的string类得功能也非常强大的,有赋值、比较、交换等等。(目前位置用的较少,补充待续)
在具体的问题中,我目前为止还有一个问题未得到解决:如何将一个字符 a 接到一个字符串 s 的尾部去。现有的 strcat() 等方法都是针对 char * & char * 操作的,我后来还试着尝试了先赋值给一个 char * 对象,然后再用 strcat() 等,但是还是会出现一些乱码等现象(python可能会比较好解决,直接可以取指定区间的子字符串)。
质数求法及 a trick
一般求质数方法就是判断数 n 在 sqrt(n) 中只存在因子 1,则 n 是素数。但是有时候这种求法在某些算法题目中时间占用太多,比较好的优化方法是使用筛选法。
求 n 以内的所有质数:
int isprime[n];
memset(isprime, 1, sizeof(isprime));
for(i = 4; i <= n; i += 2) {//筛掉大于2的偶数
isprime[i] = 0;
}
len = sqrt(n);
for(i = 3; i <= len; ++i) {
if(isprime[i] == 0) {
continue;
}
step = i << i; //筛掉大于质数 i 的所有非质数
for(j = i * i; j < n; j += step) {
isprime[j] = 0;
}
}
上述代码中 isprime[i] == 1 时,表示 i 即是一个质数。个人觉得代码中的精华应该是 step 的赋值
step = i << i
这两天看到的一个算法题目,恰好我看了第一眼就觉得是求质数,但是,后来总是time out,甚至 error。题目贴出来如下:
Iahub and Iahubina went to a date at a luxury restaurant. Everything went fine until paying for the food. Instead of money, the waiter wants Iahub to write a Hungry sequence consisting of n integers. A sequence a1, a2, ..., an, consisting of n integers, is Hungry if and only if: 1)Its elements are in increasing order. That is an inequality ai < aj holds for any two indices i, j (i < j). 2)For any two indices i and j (i < j), aj must not be divisible by ai. Iahub is in trouble, so he asks you for help. Find a Hungry sequence with n elements. Input The input contains a single integer: n (1 ≤ n ≤ 10^5). Output Output a line that contains n space-separated integers a1 a2, ..., an (1 ≤ ai ≤ 10^7), representing a possible Hungry sequence. Note, that each ai must not be greater than 10000000 (10^7) and less than 1. If there are multiple solutions you can output any one. Sample test(s) Input 3 Output 2 9 15
仔细分析这个题目,其实只是一个小 trick,特别要分析上述题目中给的范围。
(注:第 10000000 个素数是 1299743;Note:101 % 100 != 0)。
最大公约数和最小公倍数小结
这个问题每个人都能很好的解决,但是很久没搞算法这一块,都忘了,所以在这里记录,方便以后温故而知新。
欲求最小公倍数,可以先求出最大公约数。而求解最大公约数的最简方法在数论中称辗转相除法,也叫做欧几里得算法。该算法不需要因式分解。
具体代码段如下(gcd 为最大公约数,lcm 为最小公倍数):
total = m * n;
while(n) {
tmp = m % n;
m = n;
n = tmp;
}
gcd = m;
lcm = total / gcd;
或者如代码段:
gcd(int a, int b) {
return b == 0? a: gcd(b, a % b);
}
最大公约数可以这么求证明如下:
假设 a % b = t,则 a = kb + t;我们可以知道 t 和 a、b 的最大公约数是一致的,因为 a = m(gcd), b = n(gcd),上述式子进一步可以表示为 m(gcd) = kn(gcd) + t,则 (m - kn)gcd = t。所以求解 a 和 b 的最大公约数之需要求 b 和 t 的最大公约即可,如此下去,最后当 t = 0 时,结束查找,即可找到两者的最大公约数;得证。
老人摔倒,扶,还是不扶?
最近几年经常看到“老人摔倒,该不该扶?”一类的报道及大家对此展开的讨论,其中说法各异,虽然不少言辞渗透出负面的信息,但由此类展开的关于社会、法律和道德等方面的讨论却引起了我的深思。
从2006年的“彭宇案”,到前不久四川达州声称被三个小孩推倒的老太太蒋某系自己摔倒案件,这期间类似的事件发生了多起。看到一位老人跌倒在身边,你扶,还是不扶?如今这个问题让很多人都陷入了纠结,伴随着恩将仇报的见义勇为、惹祸上身的助人为乐使得传统美德陷入了一种莫名的尴尬。特别是“彭宇案”、“许云鹤案”的判决结果,让很多公众在此事上都表现出负面的情绪。
但我们有没有深入思考过这类案件产生的原因,或者将视角深入到更高层面去看待这类问题?
是老人坏了,还是坏人老了?
随着近些年经济发展步伐的加快,很多社会问题都浮出水面,人口红利带来的经济发展模式受到挑战,社会的老年化问题越来越严重,一方面社会养老压力加大,特别是城乡老人收入水平较低,增长慢,另一方面老人服务和养老方式不够完善,医疗保险覆盖率低,农村缺医少药。在这样的大背景下,陆续出现了“彭宇案”,看到一个老人跌倒,从道德上讲,我们应该路见不平施以援手,但是当你伸出手时,不该有的事情发生了,所有的事情都要你一个人扛,这样的情况下,救助者都会左右为难,无从下手。
当今社会,是老人坏了,还是坏人老了?
针对此事件,我们从结果分析其本质。老人指助人者为肇事者,或者没事而谎称有事,最后无不是因为找不到真正的肇事者而需要担负医药费,或趁机讹诈一笔改善生活等。老人们这些纯粹的目的,无疑应引起我们深刻的思考。如果老人们生活在一个社会保障系统健全的社会,其权益、生活、医疗等都有真正落实到位的保障,这类的时间还会发生么?
再从案件结果出发,如果一个社会有完善的法律程序、道德指南,就不会出现“彭宇案”等让人面对老人摔倒事件望而却步的判决结果。没有撞人并做了好事却要上法庭,且没有证人的情况下被判定为要付法律责任,又怎么不让人产生负面的情绪,唤起人们以后从道德角度进行施救呢?
在围观中思考如何搀扶正义
老人跌倒,我们理应该出手时就出手,而不应该采取事不关己,高高挂起态度。继这类事情发生之后,我们该如何在围观中搀扶正义?
政府相关部门应该颁发更健全的社会保障体系,特别是针对当前老年化问题日益突出的社会,除了保障体系,更重要的是将具体政策落实到位,在落实过程中可以采取监管等措施。
国家应该修订相关法律,让摔倒事件得到公平公正的处理,不能因为是老人就享有做错事情而不受惩罚的权利,也不能因为片面之词就错判好人。相关公益网站对此类事件产生的官司,可以提供免费的法律援助等。
人之初,性本善,我们应该要坚信人性之美,传承中国的传统美德,不能因为个别事件而“废食”。在具体实施帮助的时候,可以先分析情况,如果老人意识清楚,就问询老人跌倒情况及对跌倒过程的记忆,如果不能记忆,可以记录自己的帮助过程、打电话急救等等。
结语
老人跌倒,扶还是不扶的纠结,归根结底是社会保障的不健全、法律的缺失及道德的退步。我们要解决这类问题,必须从健全并落实完备的社会保障系统、修补法律漏洞和大力弘扬传统美德等方面出发,才能从根本上解决这些问题,才能在社会上唤起人间的正义、社会的公平,让整个社会呈现出一片和谐和关爱。