Galois 域上运算实现与优化归纳
此文主要就 Galois 域上的运算方法及其优化进行归纳总结:
Galois 域及运算在很多领域都有很好的应用,特别是信息的加解密、数字签名、存储系统的编码等。所以底层 Galois 域运算的效率至关重要。Galois 域内的运算有加减乘除四种,而乘除所花费的代价是最多的,所以针对 Galois 域上运算的优化主要是针对乘除来说的。
方法一:基于 log/antilog tables 的 look-up tables (上一篇文章有所论述):

方法二:full-multiplication table (full look-up table):
log/antilog tables 这种方法中用到了三次查表操作,基于此较好的优化方法是将有限域内所有元素的乘积都存储在表格中,即 full look-up table,此时之需要一次查表操作即可完成。但是此方法有一个明显的缺陷:针对 $w$ 较小的情况是可行的,但是当其增大时,表格所需的存储空间也会以指数形式增大,当 $w = 8$ 时,需要 64KB,当 $w = 16$ 时,需要的空间为 8GB,目前位置的计算机内存空间显然满足不了要求。
方法三:针对 log/antilog tables 的优化:
标准的 log/antilog tables 算法只要两个检验 $0$ 分支,三个查表操作,一个加法和取模操作。基于此,Huang 和 Xu 提出了三种优化方法:
1. 通过元素移位替代取模操作,如下(首先仍要判断是否为 $0$)
$$antilog[(log[a] + log[b]) & (2^n - 1) + (log[a] + log[b]) >> n]$$
2. 通过扩大 antilog table 替代取模操作,具体就是将该 table 扩展到 $-2^l + 1$ 到 $2^l - 2$,进而直接查表即可(首先仍要判断是否为 $0$)。
$$a * b = antilog[log[a] + log[b]]$$
3. 取消是否为 $0$ 的分支判断,和 Broder 的方法一样:
要取消分支判断,可以通过进一步扩大 antilog table,使元素 $0$ 在运算时得到映射。假设令 $logf[0] = 2Q$ (其中 $Q = 2^w$),则进行如下操作:
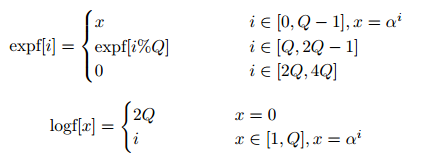
最后对应的代码是:

方法四:double tables or left-right table:
该中方法主要是针对 full multiplication table 而言的优化,原者的缺点是在 $w$ 较大的情况下,现有内存满足不了要求,故此方法就是退而将空间减小。两个元素 $a(x) = a_1 + a_{2}x + ... + a_{l - 1}x^{l - 1}$ 和 $b(x) = b_1 + b_{2}x + ... + b_{l - 1}x^{l - 1}$ 属于 $GF(2^l)$,则将两者相成具体可以表示为:
$$a(x) * b(x)
= (a_1 + ... + a_{l - 1}x^{l - 1}) * (b_1 + ... + b_{l - 1}x^{l - 1})
= ((a_1 + ... + a_{\frac{l}{2} - 1}x^{\frac{l}{2} - 1}) *
(b_1 + ... + b_{l - 1}x^{l - 1})) + ((a_{\frac{l}{2}}x^{\frac{l}{2}}
+ ... + a_{l - 1}x^{l - 1}) * (b_1 + ... + b_{l - 1}x^{l - 1}))$$
这样优化可将原来需求的 $2^l * 2^l$ 空间减小到 $2^l * 2^{\frac{l}{2}}$。对应的实现可以表示成如下:

方法五:使用 composite fields:
如其名,该方法主要是将运算的基底改变,基于较小的域来实现较大域的运算。即 $GF(2^n) = GF((2^l)^k)$,其中 $n = l * k$。进一步我们可以称 $GF(2^n)$ 是基于 $GF(2^l)$ 、度为 $k - 1$ 的多项式的集合。根据有限域运算的规则,现在的问题是需要找到一个基于 $GF(2^l)$ 的度数为 $k$ 的本源多项式 $f(x)$,现有的 Ben-Or 算法是一个比较有效的寻找本源多项式的算法,以 $GF((2^l)^2)$ 为例说明:
此时得到的本源多项式为 $f(x) = x^2 + s*x + 1$,该域中的两个元素 $a_1x + a_0$ 和 $b_1x + b_0$,两者相成可以表示成:
$$(a_1x + a_0) * (b_1x + b_0) = a_1b_1x^2 + (a_1b_0 + a_0b_1)x + a_0b_0$$
根据本源多项式有 $x^2 = sx + 1$ mod $f(x)$,则上式可以表示成
$$(a_1b_0 + a_0b_1 + sa_1b_1)x + (a_1b_1 + a_0b_0)$$
所以在 $GF((2^l)^2)$ 上的乘法运算主要是基于 $GF(2^l)$ 的五个乘法运算。此时空间得到了大量节省,但是需要计算额外的多个乘法,特别是当域增大时,乘法数量可能还会增加,这样到最后得到的性能可能会有所降低。
在 composite fields 上的求反运算最快的方法是使用 Extended Euclidean Algorithm。
(PS:在加解密中,域的大小会影响安全度,所以对大域的研究主要集中在这个应用中)
方法六:2-D table look-up:
这算是一种比较自然的想法,将乘法结果和除法结果都分别放置到二维表格中,具体计算时直接查表即可。
最后还要提一下很多论文中都会出现的一个表格:
| Space | Complexity | |
| Mult. Table | $2^l * 2^l$ | 1 LKU |
| Lg/Antilg | $2^l + 2^l$ | 3 LKU, 2 BR, 1MOD, 1 ADD |
| Lg/Antilg Optimized | $5 * 2^l$ | 3 LKU, 1 ADD |
| Huang and Xu | $2^l + 2^l$ | 3 LKU, 1 BR, 3 ADD, 1 SHIFT, 1 AND |
|
LR Mult. Table |
$2^{\frac{3l}{2} + 1}$ | 2 LKU, 2 AND, 1 XOR, 1 SHIFT |
上面给出了基于 Galois 域上多种运算和其优化的方法,根据相关论文的调查,这么多方法的性能在不同的应用情况下是不同的,底层性能和上层性能不是成正比例的关系,同时实验环境的层次以及测试数据的组织形式都会影响性能。
PS:现有比较知名的 lib 是 James Plank 给出的 fast Galois field lib,该 lib 主要集中实现了 $GF(2^8), GF(2^{16}), GF(2^{32})$ 的运算。优化方法使用到的比较少。
2022年9月11日 16:00
Mathematics is one of the tough subjects and also an easy subject for class 10th standard students of TM, EM, AP 10th Maths Model Paper UM and HM studying at government and private schools of the state. Department of School Education and teaching staff of various institutions have designed and suggested the Mathematics question paper with solutions for all chapters topic wide for each lesson of the course, and the AP SSC Maths Model Paper 2023 Pdf designed based on the new revised syllabus and curriculum.