摘录
有时候觉得有些话、有些内容挺让人受启发的,这种启发是各方面的,其影响甚至可以受用一生。当我们烦躁不安时,静心品读,或许生命又会被着上别样的色彩。集中做一下摘录如下:
1. 如同分析代码,只看输出的总体时间是难以优化的,关键是整个过程的不同阶段的耗时(注意二八定律);
2. 金融的本质是永远用你的钱,为比你更有钱的人服务。
索罗斯投资理念是:量子最基本的特征是无论怎么改变实验方式、观察技术,都不可能改变量子轨迹的不确定性。
——《世界是一部金融史》
3. 这些年,我发现学历跟人生快不快乐没有什么关系,重点是一个人的生活态度:能不能幽默的看待自己以及这个世界。
阿拓总能用十年后的心态来看待眼前的事物,这就是为什么他好脾气的原因。如果你每一次遇到事情都能跳出来,用一种更成熟的眼光来审视,可能很多事情都会豁达很多。
——《等一个人咖啡》
4.人与人的差别就是习惯的差别:如果一时间作为坐标横轴,每天的习惯好坏按分支高低作为纵轴,对时间轴进行积分的话,最终的面积结果就是一个人一生的成就总量,你会发现,和他人一丢丢的习惯上的微小差距,在岁月的作用下,成就的面积差距是如此的巨大。因此,任何一个有非凡成就的人,从外界看,可能会有很多机缘,但从内功来看,这些习惯一定是不可或缺的,并非偶然。
(未完待续)
Ubuntu 右上角小键盘不见了解决方法
好久没用电脑了,打开电脑,发现发现输入法不能切换且 ubuntu 右上角的小键盘不见了,再网上搜索方法如下:
打开终端,在终端里输入如下命令:
1. killall ibus-daemon
2. ibus-daemon -d
ibus 输入法偶尔会挂掉,结束进程,再重新启动即可。
Galois 域上运算实现与优化归纳
此文主要就 Galois 域上的运算方法及其优化进行归纳总结:
Galois 域及运算在很多领域都有很好的应用,特别是信息的加解密、数字签名、存储系统的编码等。所以底层 Galois 域运算的效率至关重要。Galois 域内的运算有加减乘除四种,而乘除所花费的代价是最多的,所以针对 Galois 域上运算的优化主要是针对乘除来说的。
方法一:基于 log/antilog tables 的 look-up tables (上一篇文章有所论述):

方法二:full-multiplication table (full look-up table):
log/antilog tables 这种方法中用到了三次查表操作,基于此较好的优化方法是将有限域内所有元素的乘积都存储在表格中,即 full look-up table,此时之需要一次查表操作即可完成。但是此方法有一个明显的缺陷:针对 $w$ 较小的情况是可行的,但是当其增大时,表格所需的存储空间也会以指数形式增大,当 $w = 8$ 时,需要 64KB,当 $w = 16$ 时,需要的空间为 8GB,目前位置的计算机内存空间显然满足不了要求。
方法三:针对 log/antilog tables 的优化:
标准的 log/antilog tables 算法只要两个检验 $0$ 分支,三个查表操作,一个加法和取模操作。基于此,Huang 和 Xu 提出了三种优化方法:
1. 通过元素移位替代取模操作,如下(首先仍要判断是否为 $0$)
$$antilog[(log[a] + log[b]) & (2^n - 1) + (log[a] + log[b]) >> n]$$
2. 通过扩大 antilog table 替代取模操作,具体就是将该 table 扩展到 $-2^l + 1$ 到 $2^l - 2$,进而直接查表即可(首先仍要判断是否为 $0$)。
$$a * b = antilog[log[a] + log[b]]$$
3. 取消是否为 $0$ 的分支判断,和 Broder 的方法一样:
要取消分支判断,可以通过进一步扩大 antilog table,使元素 $0$ 在运算时得到映射。假设令 $logf[0] = 2Q$ (其中 $Q = 2^w$),则进行如下操作:
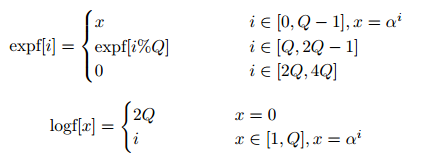
最后对应的代码是:

方法四:double tables or left-right table:
该中方法主要是针对 full multiplication table 而言的优化,原者的缺点是在 $w$ 较大的情况下,现有内存满足不了要求,故此方法就是退而将空间减小。两个元素 $a(x) = a_1 + a_{2}x + ... + a_{l - 1}x^{l - 1}$ 和 $b(x) = b_1 + b_{2}x + ... + b_{l - 1}x^{l - 1}$ 属于 $GF(2^l)$,则将两者相成具体可以表示为:
$$a(x) * b(x)
= (a_1 + ... + a_{l - 1}x^{l - 1}) * (b_1 + ... + b_{l - 1}x^{l - 1})
= ((a_1 + ... + a_{\frac{l}{2} - 1}x^{\frac{l}{2} - 1}) *
(b_1 + ... + b_{l - 1}x^{l - 1})) + ((a_{\frac{l}{2}}x^{\frac{l}{2}}
+ ... + a_{l - 1}x^{l - 1}) * (b_1 + ... + b_{l - 1}x^{l - 1}))$$
这样优化可将原来需求的 $2^l * 2^l$ 空间减小到 $2^l * 2^{\frac{l}{2}}$。对应的实现可以表示成如下:

方法五:使用 composite fields:
如其名,该方法主要是将运算的基底改变,基于较小的域来实现较大域的运算。即 $GF(2^n) = GF((2^l)^k)$,其中 $n = l * k$。进一步我们可以称 $GF(2^n)$ 是基于 $GF(2^l)$ 、度为 $k - 1$ 的多项式的集合。根据有限域运算的规则,现在的问题是需要找到一个基于 $GF(2^l)$ 的度数为 $k$ 的本源多项式 $f(x)$,现有的 Ben-Or 算法是一个比较有效的寻找本源多项式的算法,以 $GF((2^l)^2)$ 为例说明:
此时得到的本源多项式为 $f(x) = x^2 + s*x + 1$,该域中的两个元素 $a_1x + a_0$ 和 $b_1x + b_0$,两者相成可以表示成:
$$(a_1x + a_0) * (b_1x + b_0) = a_1b_1x^2 + (a_1b_0 + a_0b_1)x + a_0b_0$$
根据本源多项式有 $x^2 = sx + 1$ mod $f(x)$,则上式可以表示成
$$(a_1b_0 + a_0b_1 + sa_1b_1)x + (a_1b_1 + a_0b_0)$$
所以在 $GF((2^l)^2)$ 上的乘法运算主要是基于 $GF(2^l)$ 的五个乘法运算。此时空间得到了大量节省,但是需要计算额外的多个乘法,特别是当域增大时,乘法数量可能还会增加,这样到最后得到的性能可能会有所降低。
在 composite fields 上的求反运算最快的方法是使用 Extended Euclidean Algorithm。
(PS:在加解密中,域的大小会影响安全度,所以对大域的研究主要集中在这个应用中)
方法六:2-D table look-up:
这算是一种比较自然的想法,将乘法结果和除法结果都分别放置到二维表格中,具体计算时直接查表即可。
最后还要提一下很多论文中都会出现的一个表格:
| Space | Complexity | |
| Mult. Table | $2^l * 2^l$ | 1 LKU |
| Lg/Antilg | $2^l + 2^l$ | 3 LKU, 2 BR, 1MOD, 1 ADD |
| Lg/Antilg Optimized | $5 * 2^l$ | 3 LKU, 1 ADD |
| Huang and Xu | $2^l + 2^l$ | 3 LKU, 1 BR, 3 ADD, 1 SHIFT, 1 AND |
|
LR Mult. Table |
$2^{\frac{3l}{2} + 1}$ | 2 LKU, 2 AND, 1 XOR, 1 SHIFT |
Galois 域上的运算(规则)
考虑到存储编码中,矩阵等之间的运算都是在伽罗华域(Galois Field,GF,有限域)上进行的,所以要实现底层的运算库,必须了解 GF 上的运算规则。开始前,我们将字长设为 $w$ bit。
GF 上的加法和减法运算比较简单,都是两个数值直接异或( XOR )。对乘法和除法运算,很多人可能会想到,首先按照十进制进行乘除运算,然后再将结果模上 $2^w$ 即可。这样做我们容易得到,GF 上的数值都是成对出现的,但是当 GF($n$) 中的 $n$ 不是质数时,不能构成 pairs,另外对类似于 $(3/2) \% 4$ 的运算时没有定义的,综合上面所论述的,所以 GF($2^w$) 上的乘除法运算不能简单做如上定义。
GF($2^w$) 的乘除法运算规则使用到了线性代数中用最小多项式简化高次矩阵运算的理论,简单说来就是“除法原理”。我们定义 GF($2^w$) 上关于 $x$ 的多项式,即若 $r(x) = x + 1, s(x) = x$,则有 $$r(x) + s(x) = x + x + 1 = (1 + 1)x + 1 = 1$$
根据“除法原理”,有 $r(x) = q(x)t(x) + s(x)$,即 $r(x) \% q(x) = s(x)$ ($q(x)$ 除 $r(x)$ 的商是$t(x)$,余数是$s(x)$),同时,易知 $s(x)$ 的度($x$ 的最高次)要小于 $q(x)$ 的。
我们设 $q(x)$ 是在 GF($2$) 上对应度为 $w$ 的本原多项式(最小多项式),则任意的 GF($2^w$) 均可以由 GF($2$) 下的多项式 $x$ 产生出。基本步骤是:
1. 给定一个初始集合 $\{0, 1, x\}$;
2. 将这个集合中的上一个元素,例如 $x$ ,乘以 $x$ ,如果得到的结果的度大于等于 $w$,则再将结果 mod $q(x)$;
3. 直到集合有 $2^w$ 个元素,此时最后一个元素乘以 $x$ 再 mod $q(x)$ 的值为 $1$。
下面给出一个例子来说明,当 $w = 2$ 时,$q(x) = x^2 + x + 1$,对 GF($4$),最开始的集合是 $\{0, 1, x\}$,这个集合的上一个元素是 $x$,乘以 $x$ 得到 $x^2$,此时其度等于 $w$,所以 $x^2 \% q(x) = x + 1$;此时集合更新为 $\{0, 1, x, x + 1\}$;再将 上一个元素 $x + 1$ 乘以 $x$,得到 $x^2 + x$,其度数也等于 $2$,所以 $(x^2 + x) \% q(x) = 1$,此时可以结束这个过程,即 GF($4$) 为 $\{0, 1, x, x +1\}$。
通过上面说明,只需要找到对应 GF($2^w$) 上的本源多项式 $q(x)$ (运算遵循 GF($2$)),则其即可通过 $x$ 代换得到,可以对应表示成:$$GF(2^w) = GF(2)[x] / q(x)$$
根据已有理论,根据不同 $w$ ,对应本源多项式为:
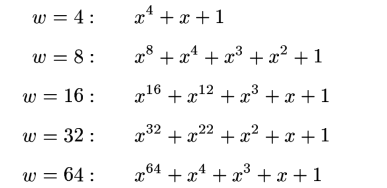
在实际计算机中,都是使用二进制来运算,所以我们需要将 RS 码中的 GF($2^w$) 中的元素都映射到二进制上来:$s(x)$ 的元素 $x^i$ 对应到二进制位的 $i$ -th,例如上面的 GF($4$) 中,依次对应的是 $\{00, 01, 10, 11\}$。如下图给出 GF($16$) 的例子:
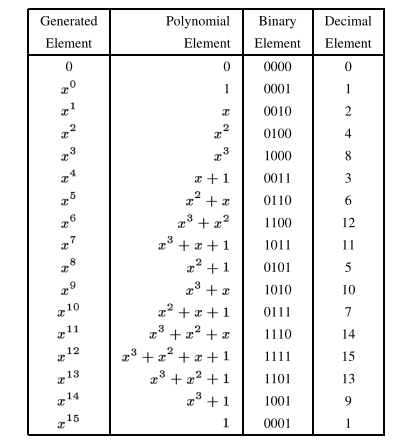
通过上面系列对 GF($2^w$) 的分析,对应其上的乘法可以转换成多项式相乘后再 mod $q(x)$,问题得到了简化(多项式相乘时,各元素次数做的是加法)。因此,我们定义 RS 码上的元算时,先将二进制映射成多项式,再求模运算,再转换成二进制,这样一来,我们有两个映射表格 gflog(将二进制映射成多项式) 和 gfilog(对多项式进行运算,然后将结果转换成二进制),不同的 $w$ 对应不同的表格,表格中的元素是 $2^w - 1$ ($0$ 单独存在,没有哪个的次方等于 $0$)。如下图给出了$w = 4$ 情况下的两个表格:

对应给出几个乘法和除法运算的例子:
7 * 9 = gfilog[gflog[7] + gflog[9]] = gfilog[10 + 14] = gfilog[9] = 10
13 / 11 = gfilog[gflog[13] - gflog[11]] = gfilog[13 - 7] = gfilog[6] = 12
转:程序员遇到bug时常见的30种反应
开发应用程序是一项压力很大的工作,人无完人,工作中遇到bug是很正常的事,有些程序员会生气,沮丧,郁闷,甚至泄气,也有一些程序员则会比较淡定。如何进行修复bug的过程,是值得我们好好推敲的。
我想分享一些有关程序员在努力修复bug时常说的话和冒出的想法。当氛围变得紧张的时候,这些话就会显得轻松幽默。最终,bug也会修复成功,你将会继续下一个任务。
我相信许多web开发人员和软件工程师在编程中都会遇到困难,而事后回想起来,还会觉得很好笑。
1、我不知道该删掉还是重写
回归曾经写的源代码,总有一种想要重新返工的冲动,逻辑性差,冗余代码多,让人难以理解。但是,如果功能没出现问题,千万不要去修改。这是我经常要面对的困扰,相信也困扰了其他不少的软件开发者。
2、一开始架构时就该查Github
相信绝大多数开发人员都知道Github,它上面每天都会发布的一些神奇的开源项目。所有语言的程序员都会利用网络,为已存在的项目创建分支,添加项目wiki描述,或者创建自己的代码库,这些都为各种各样的项目的插件和模板提供了很多丰富的资源。
3、为什么这个脚本要依赖这么多库
说到一些越来越被广泛使用的计算机语言,像Java和Objective-C,库文件的数量也不断增加。很明显可以看出,构建一个框架就需要许多的基础库,甚至一些JavaScript的插件也需要很多大量的附加文件。有时候这些乱七八糟的东西会很让人心烦,但是至少它能运行。
4、网上一定有解决办法
遇到困难时,我的第一反应就是上网查资料,很多程序员会在论坛上发布他们的问题,最终这些问题都会被解决并存档。Google会很神奇地选择一些跟你的问题相关的关键字,你就能够轻而易举地得到一些对你有帮助的讨论信息。不幸的是,有时候对于一些特定的问题,相关的信息还不是很多。
5、有这个功能的插件吗
何必要多此一举插件是扩展任何程序或者网站用户接口的很好的资源。另外它们还为开发者提供了一些定制以及独特的选项。如果没有可用的插件,那你为什么不自己创建一个呢?
6、对于网站项目,我好担心坑爹的InternetExplorer
使用IE渲染网页遇到的各种困难,我就不提了,从5。5版本到IE9-IE10,对于浏览器的支持问题的争议就一直不断。Web开发人员会很害怕网页调试,使用IE6进行渲染更是噩梦。,幸好那些日子已经慢慢成为历史了。
7、有些逻辑语句,并不符合逻辑
有一些逻辑语句,像if/else循环,for循环,while循环,do循环…等等,还有很多。在回顾一些源代码时,我总是尽力想弄明白我的逻辑是怎么回事。我经常会回头更新代码,让逻辑更清晰。
8、我花30分钟写个函数,运行它却要花2个小时
这不是十年前的一个有关编程的故事吗?当一切都在按照你所所期待的顺利进行着,突然某个函数输出了一个致命的错误,所以你不得不回头删除代码块,试图定位出错的代码行。尽管这会让你筋疲力尽,但是一旦找到错误的原因,问题解决之后,你又会立马感到浑身轻松。
9、读了几篇博客后,我才意识到我之前所做的全是错的
我总是喜欢根据自己的编程思想直入主题,但是如果事情没有按照我原本的计划进行时,会导致很多麻烦。有很多次,我在做项目时,途中都遇到了麻烦,最后只得查找博客和相关文章去寻求帮助。然后又发现我的整个方法完全错了,还不如从头开始更容易点。所以从长远来看,在项目开始时多做点研究反而会节省时间。
10、StackOverflow上有好心人或许能帮助我
我已经数不清有多少次,遇到问题都是通过StackOverflow得到解决的。只要你提出问题,社区里就会有很多聪明,友好的热心人愿意帮助你。所有的在线论坛里,它绝对是支持软件编程和前后端web开发的最全面的网站。
11、这个问题竟然就因为少了个右括号
调试是我们经常要用的方法,向前两步,回退一步,再向前两步,如此反复。为了查找函数命名或者变量作用域等错误,盯着代码看了数个小时,结果发现只是缺少了一个括号,你会有种哭笑不得的感觉。所有的时间都浪费在了一个小小的语法错误上,那一刻,你会觉得自己既是天才,又是傻子。
12、喝杯咖啡,休息一下
有的时候你需要起身离开显示器,连续敲了几个小时的键盘,如果中间休息一下,会对你的身体有益。大多数健康指南都建议每30-60分钟休息一次。但是还是要取决于你的需要,如果你感觉中间暂停去休息会打断你的思维,让你很不爽,那就最好不要了。
13、我应该先把这个项目放一放,稍后在处理它
休息的另一种方式就会暂停你手中的项目,而不是离开你的电脑桌。或许你还有其他的工作要做,那就继续下一项任务。比起试图在一个花了5个小时还没解决的问题上继续挣扎,这会是一种更合理地分配时间和资源的方式。
14、我在想或许古典音乐能够激发我的编程潜能呢
有一种说法认为古典音乐能促进植物的早期生长,我个人更偏爱古典音乐错综复杂的注解和音乐理论。爵士,钢琴,大型乐队,优雅的音乐在全球各地的人类文化都占有一席之地。所以编程的时候听点美妙的音乐会让你调试起来更得心应手呢。当然也有可能,会让你更加心烦意乱。
15、或许现在是验证鲍尔默峰值理论的好时机
我相信很多读者都知道鲍尔默峰值,它是根据一个特殊的XKCD漫画得来的。简单来说,这个理论认为程序员的编码能力在喝了定量的酒后,会达到一个峰值。这个起源于SteveBallmer的些古怪滑稽的姿态被认为是像一个醉汉在说胡话。尽管这有点讽刺,因为鲍尔默在微软从来算不上一个真正的程序员,猜想我们只有等其他人来实践这个理论了。
16、是谁动了我的代码?
这个听起来有点像妄想症,但是有时候你很想知道是谁趁你补觉的时候写的这些东西。回顾过去几周或者几个月的项目,会给你一种晕乎乎的感觉。有时候你会不记得你写过这些东西—尽管上周你还在参与这个项目。好像是我很疯狂地写的代码,你却从来不知道…
17、完全不知道这是神马东东
你遇到的最糟糕的情况应该是在研究源代码时,完全不知道它是在干什么,可能是来自你自己的项目,也可能是其他人的项目,但是问题都一样。这个时候,你必须确定是否值得花费更多的时间去寻找其它解决方案或者仔细剖析代码,研究它到底是干什么的。
18、直接google下错误提示
鉴于多年的PHP经验,我不得不说Google真的是调试问题的最好的小伙伴。这对于Objective-C,C++,Java和其他的主流语言的境况一定是相同的。错误提示信息对我们很有用,但是你必须记住不同的错误代码代表什么意思。它读起来更像是被翻译过的计算机语言。幸好有这么多在线支持,让我们确定这些错误信息代表的真正意思。
19、今天应该到此为止了,可我真的想把这个问题解决了
我们都知道想要退出时的那种极度沮丧的感觉,但是同时又觉得放弃不是正确的选择。你很想继续前进,找出新的解决方案来。但是如果到最后还是浪费了一个小时,那该怎么办?我对这种情况并不陌生,它会让人特别沮丧。
20、哦买糕的,为什么我都没写注释呢
如果涉及到最基本的前端代码HTML/CSS/JS时,并不需要总是写注释。但是如果是比较复杂的脚本和程序时,就需要写一些标准的注释以便你几个月,甚至几年后来重温这些代码。有时候你会忘记给函数,参数,输出格式以及其他重要的数据写注释,这无疑会导致发生bug时你不得不调试整个脚本去寻求解决方案,感到非常困惑,到那个时候你会觉得要是有一些有用的注释该多好啊。
21、这个20分钟之前还好好的呢
或许构建程序时最让人沮丧的是,明明刚才还好好的东西,没有改过任何代码,这会儿却运行不起来了。我发誓这种情况绝对有发生,而且它没有任何意义—也许其它程序运行的是缓存版本呢然后也有一些时候我们只更新了一丁点代码,结果整个程序都崩溃并且完全停止运行。那就会回退到最新的备份版本,从那儿继续吧。
22、忘了一个该死的分号,整个程序都崩了
几乎我用过的所有的编程语言都要求每行结束时都要有结束符,但并不是所有的语言都这样,不过C/C++系列语言绝对是这样。当你忘记添加分号结束符时,这是多明显的错误!但是解析器并不不理解,便抛出一个致命的错误。接下来就得再花费20分钟时间去研究代码,查找技术错误。最终发现只是少了一个分号。哈,这就是软件调试的乐趣。
23、我想要招人来帮我修复bug,得花多少钱哪
雇佣程序员的想法听起来很诱人,但显然在经济上是不可行的。另外,如果你连自己的的错误都没解决,你又怎么能从这些错误中学到东西呢?经历多次失败,最后当你真正理解了编程的概念后,你会很有成就感。但有时候脑子里难免还是会闪过这种想法。
24、快速浏览下HackerNews,肯定能提高我的效率
很多程序员对于浏览软件和创业等社会新闻的偏爱选择都是HackerNews首页。它有大量的关于自由职业,时间管理,软件开发,创业发布和筹资资金等方面很棒的信息。尽管HN能够模拟出通过自我教育更加高效的感觉,但其实是在浪费你的时间。每隔几小时去快速浏览下新闻也没那么糟糕。
25、这个API怎么没有说明文档啊?
最让人沮丧的事情就是使用插件或者框架时,自带的文档很糟糕,你只好自己去深入阅读源代码。我更喜欢让开发人员花时间专门为项目设计一个文档页,对所有的参数和选项都给予解释,有可能的话,给出一些示例代码。但是很遗憾,这种情况几乎不可能。所以最简单的办法就是远离那些附带文档很糟的工作,以免给自己带来麻烦。
26、我真希望我已经对数据库进行备份了
在编写和调试代码的时候,我有时候会想不到备份。然而,数据备份能够帮助我们回退到做出某个特定的改变之前的版本,这对一个即时的服务器环境是特别有用的,有些变化瞬间就会发生。切记在本地保留对网站文件和数据库的拷贝,以备急需。你可能会觉得这样太麻烦了,但是总比你重建一个SQL数据库强多了。
27、怎样才能快速解决这个问题?
如果花费了数小时后,仍然未找到一个解决办法,很明显你需要一个新的方案了。程序员总是想要先实现功能,然后再去设计和美化界面。先确定一个最快的,最准确的解决方案,并尽力去实现和完成,然后再去考虑美化界面的问题就会很轻松了。
28、我敢打赌,你更新下我的代码,这个问题就解决了
那些为编程语言提供依赖包和插件的团队并不需要频繁地发布产品。有时候从本地传送文件到服务器的时候,更新PHP/Ruby/Python/SQL版本可能会解决一些调试问题。除非你的版本实在太旧了,否则本地更新很少能够帮助你修复源代码中的bug,不过还是值得一试!
29、我真的该好好学习Git了,…还是下周吧
开源的版本控制控制软件Git在程序员中广受欢迎。跟其他竞争对手相比,它提供了一条更简单的学习曲线,被应用在了许多在线仓库像Github和Bitbucket中。可能对初学者来说,会有点难度,但是一旦你掌握了基本命令,你会发现使用GIt就是小菜一碟。它还让版本控制更加清晰。
30、算了,我还是从头开始吧
有时候尝试了数小时的解决方案后,你可能需要将你的工作文件归档(或者删掉它们),重新开始。这个决定的最大难点就是你会考虑到前面数小时的工作会毫无收获。但是如果你保留之前的想法,项目却毫无进展时。重新开始,才有可能让项目顺利完成。
原文链接: hongkiat 翻译: 伯乐在线 - JingerJoe
译文链接: http://blog.jobbole.com/49756/
A Study of Linux File System Evolution
这篇文章是今年由 Lanyue 等人发表的,文章深入研究了 Linux 文件系统代码的 evolution,就像将一个摄像机的镜头拉远,给我们呈现了文件系统 evolution 的全景图,有人说看了这篇文章没啥感觉,但是对于我这样的豆芽菜来说,还是蛮有收获的,所以在这里做了整理。
在开始之前,简要说明一下文件系统发展的目的:关键字 moving target、by different teams with different goals, new features、fix bugs、improve performance and reliability .etc。如果我们将镜头距离拉近,会看到,在设计一个文件系统时会有很多因素被考虑,physical journaling, logical journaling, checksumming, copy-on-write, harsh tables, indirect blocks, extent maps, data structures, asynchronous thread pools, caching, pre-allocation, stable and so on,我们在专业学习的时候都是把这些分开来一门一门的学习,但是真正综合考虑分析,我觉得我没有这个概念和模型。
文章的动机主要是考虑到本地文件系统发展的很快,要全部深入理解各个版本的基础代码往往是很费力的,或许这些个版本是有一些共性的,例如各个版本 bug 的类型是否一样,其特征化实现主要表现哪些方面等等问题。这样一来,如果我们把握了文件系统在 evolution 过程中所持有的共性以及创新,那么着对于文件系统的设计者、系统语言的设计者以及 bug 检测工具的设计者都是有很大意义的。
而文章选取 linux FS 作为研究对象主要原因有两点,一是 linux FS 的每个版本代码都是开源的,二是每个版本基本都有比较详细的分析文档。所以本文分析了这 8 年来 linux FS evolution 的 5079 个版本,其中主要涉及 Ext3, Ext4, xFS, Btrfs, ReiserFS 和 JFS(考虑到这些版本呈现了不同的特点)。
具体的研究方法是将 5079 个 FS 的版本按照其各自的特征归类,然后分析各个版本对应这些类的共有特征和区别。

上表是对 FS 分类的类型,有 5 类,通过分析,主要结论有:
1.大约 50% 的版本是代码维护和文档工作。
2.很多 bug 不仅仅在不成熟的 FS 中出现,而且在稳定版本中也普遍出现了,bug 类型和数量不会随着版本的更新而有所减少。
3.文件系统一般都有相同的逻辑组成部分,如 inode 等等。
4.具体到 Bug 类型的分析中,语义 bug 如磁盘状态、逻辑分析等是主要的 bug,超过了 50%;同步 bug 是第二多的,约占 20%,大大用户状态下软件同步的 bug;接着是 Memory bug 和 error code bug;对应的 bug 都会使 FS 崩溃或出现故障,文中具体给出了各个 bug 出现的可能原因以及引发的后果,需要特别说明的是在 FS 中,大约三分之一的 bug 是由于 failure path 引起的。
5.在 performance 版本中,主要提高这 6 个方面的效率:Synchronization(25%), Access optimization,schedule,scalability,locality and other。各个具体涉及的技术文中有说明,最后的结论是大部分文件系统版本所使用的技术都是 fairly standard。
6.在reliability版本中,主要是5个方面的改进:robust,corruption,error,annotation,debug(各种方法中对应的详细策略文中有简要说明)。大部分文件系统都有相似的 Breakdown patterns,但是根据每个版本所达到的目的不同,其在提高 reliability 时,选择策略时也会有不同的侧重。
7.文章主要使用 PatchDB 工具进行分析,主要结果如下面表格中所示。图中给出了各版本的共同点(或者改进点),其结论和上述的部分结论是一一对应的,这里不多赘述。

8.根据本文分析,虽然语义错误有难检测性的特点,但是语义错误都对应会出现不同的 bug,或 FS 会出现不同的错误,所以可以在进行语义错误工具设计时考虑检测不同的 bug 来推断语义错误。
9.虽然每个 FS 的版本初看似乎很不相同,但是如果深入下去,每个 FS 的版本基本都是近似的。
本文主要的局限是只针对 linux 文件分析,非 linux 文件的一些特征可能无法表现;对于其他版本的 linux 没有作考虑;且对于 bug 的类型,文中只讨论了被 reported 的 bug。其他相关研究工作有 operating-system bugs, user-level bugs, file-system bugs等。
综合来说,文章的贡献还是蛮大的,特别是对 FS 的设计者,bug 检测工具的设计者等有比较大的意义,“These results are brilliant in a new generation of more robust, reliable and performant file system”。另外,作者通过系列分析,还提供了一个 FS 版本的数据库供将来进一步的学习和研究:
Network Information Flow
这篇文章是 Rodolf Ahlswede 等人在 2000 年发表的一篇关于网络编码的论文。之所以把这篇论文作为我存储编码模块的第一篇论文,主要是它给我的触动还是蛮大的,真正 fire on my enthusiast for my major。
文中在摘要中指出本文真正要解决的问题以及意义。一个新的问题 network information flow(下面简称NIF) inspired by computer network apps.,那么,基于该 NIF,如何特征化可容许的 coding rate region?所以本文针对这个问题,做了一系列分析,并且最后对一个 source node 的 NIF 得到了一个简单的 coding rate region,也可以描述成 max-flow min-cut 理论。本文最大的贡献是给出并证明了通过在节点编码,也即网络编码,网络带宽能被减少。
跳过文中的铺垫,直接切入主题。当 NIF 中任一(源节点只有一个,sink 节点可以有多个) max-flow min-cut 大于等于信息源节点的信息率时,此时编码是可行的。从下面几个图以及直观的例子可以作了解(文中图 6 对该理论做了一个解释)。
当 sink 节点只有一个时,如下图。从源 s 发送 bits 至 sink 节点,终结点知道哪个 bit 是从哪个边传过来的,故可以很好的进行恢复。此时不需要编码就可以达到最优,每个 bit 会被当做一个 entity。
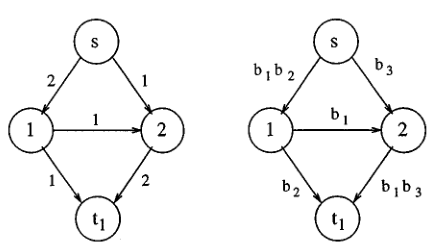
当终结点不止是一个节点时,要实现最优,网络编码也即在节点处的处理转换时不可避免的。
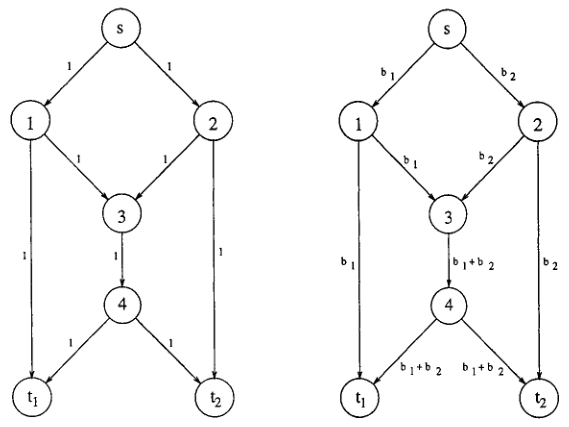
上图中给出了两个 sink 节点的情况,其中源节点到终结点 t1、t2 的 max-flow min-cut 都是 2,从源节点发送两个 bit 至终结点,在 node3 处必须又一次转换,才能最优的传送这两个节点到达终结点。
上图给出了网络编码的优势,接下来的图我们可以量化分析网络编码的优势。下图中,源节点到每个终结点的 max-flow min-cut 均为 2,此时将两个 bit 都传给这些终结点。综合分析,网络带宽为 9(边加起来),如果不用编码的方法传输,则至少还要还要一个额外的带宽才能将两个 bit 都传达给终结点,所以,最后通过使用网络编码,整体的传输带宽可以节省 10%。
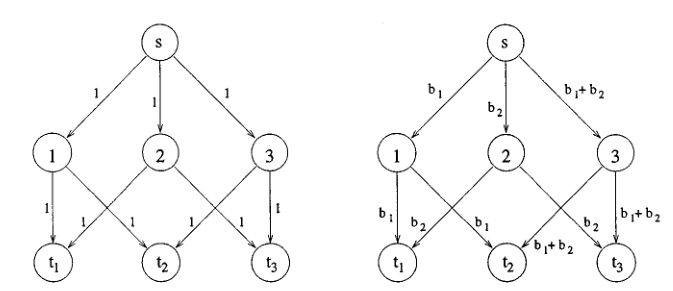
接着文章将上述结论进一步特征化,且给出一系列复杂证明(略),最后用一个 example 对特征化作了说明。而多个源节点的情况比较复杂(这类情况更加符合 P2P 网络),文章只是作了简要说明,指出要获得最优化的传输带宽,可能需要将几个源节点合并起来一起编码,不同于单个源节点的情况。
结论部分,作者重申本文的贡献(多播网络使用的传统技术并不是最优的)以及前面的 max-flow min-cut 理论。展望未来里,作者提到 multisource multisink problem 是一个非常有挑战的问题;单源节点网络中仍然存在很多问题亟待解决;带权重的图问题,我们应该多一些关注和研究(随着信息技术的发展,这确实在现今的生活中会有很大的应用,譬如一些消息是紧急的,所以较一些非紧急的消息必须有更优先的发送权,在路径的选择上,我们是否也应该专门设置一条权值较大的路?等等一系列问题)。
权威会议和期刊--(转载)
文章来源:(避免每次找博客找不到,把这篇文章转载过来)
http://www.dullgull.com/%E6%9D%83%E5%A8%81%E4%BC%9A%E8%AE%AE/
CS Conference TOP 40 计算机会议TOP40
一、A 类 15 个
- ASPLOS: Architecture Support for Programming Languages and Operation 体系结构方面的顶尖会议 微处理器设计【硬件】
- CCS: ACM Computer and Communications Security NDSS (Network and Distributed Systems Security) Web 安全方面
- FAST: USENIX Conference on File and Storage Technologies 存储领域最好的专业会议,该会议只针对存储相关的内容,属于本领域最顶级的会议。录取率非常低,现在的状况是基本上只有美国和加拿大最顶尖的研究小组在上面发表文章。每年举办一届。存储领域
- HPCA:International Symposium on High Performance Computer Architecture 高性能计算领域最好会议之一,基本上都是最顶尖的研究小组在上面发文章。高性能计算
- ICSE: International Conference on Software Engineering 软件工程方向的权威会议,接收率不到20%。除了main conference之外,还包括tutorials, workshops, symposia以及collocated conferences。编译技术
- ISCA: International Conference on Computer Architecture ISCA是由IEEE 和ACM主办的国际会议,每年一次。主要关注处理器结构、存储结构、功耗等方面的研究,在国内外学术界很高的影响。接收率20%左右。编译技术
- OSDI: USENIX Symposium on Operating Systems Design and Implementation USENIX操作系统领域重要会议,侧重操作系统各方面的新型技术。操作系统
- ACM SIGCOMM: ACM Conf on Communication Architectures, Protocols & Apps ACM的旗舰会议之一,也是网络领域顶级学术会议,内容侧重于有线网络,每年举办一次,录用率约为10%左右。网络通信领域
- ACM SIGIR: The ACM Conference on Research and Development in Information Retrieval 信息检索方面最好的会议, ACM 主办, 每年开。19%左右。信息检索技术
- ACM SIGMOD: ACM SIGMOD Conf on Management of Data 数据库与数据管理最顶级的学术会议,数据管理的主要发展都在这个会上有描述。数据管理
- SOSP:ACM Symposium on Operating Systems Principles 操作系统最好的会议和OSDI交替举行,每两年一届,操作系统旗舰会议操作系统。基本上是美国最顶尖的研究小组在上面发文章,其他地区要中极其困难。操作系统
- STOC:Annual ACM Symposium on Theory of Computing,计算机理论最权威的会议(无之一),录取率在30%左右,毕竟研究的人还是很少的,每年举行的时间不定,【2011年】【2012年】12年五月份举行。
- USENIX Annual Technical Conference USENIX的年会,操作系统、体系结构方面最好的会议之一。计算机系统
- VEE:ACM International Conference on Virtual Execution Environments
-
VLDB: The ACM International Conference on Very Large Data Bases 数据库领域顶级国际。数据库

二、B 类 25 个
- DSN:International Conference on Dependable Systems and Networks
- FOCS:IEEE Symposium on Foundations of Computer Science
- HPDC:IEEE International Symposium on High Performance Distributed Computing 高性能计算【2011】
- ICDCS:International Conference on Distributed Computing Systems 由IEEE主办,开始于1979年,从84年起每年举办一次。这是分布式计算系统领域中历史最悠久的会议。ICDCS provides a forum for engineers and scientists in academia, industry, and government to present and discuss their latest research findings on a broad array of topics in distributed computing.高性能计算
- IEEE ICDE- International Conference on Data Engineering 数据库顶级国际会议。数据管理
- IEEE ICNP: International Conference on Network Protocols IEEE 网络通信领域顶级学术会议,录用率在10%左右。网络
- ICS:Annual ACM International Conference on Supercomputing高性能计算领域的顶级会议,全世界从事高性能计算事业的每年一次的最重要的盛会之一。每年6月份召开,会上发布TOP500的上半年排名。高性能计算
- IJCAI: International Joint Conference on Artificial Intelligence 人工智能领域顶级国际会议,论文接受率18%左右。人工智能
- IEEE INFOCOM: The Conference on Computer Communications IEEE计算机和通信分会联合年会,由IEEE计算机通信技术委员会和IEEE通信协会联合举办,是信息通信领域规模最大的顶尖国际学术会议,录 用率约为16%左右。这个每年一度的会议的主要议题是计算机通信,重点是流量管理和协议。网络通信领域
- ACM SIGKDD: The ACM Conference on Knowledge Discovery in Databases and Data Mining 数据挖掘方面最好的会议, ACM 主办, 每年开。18%左右
- MICRO:International Symposium on Microarchitecture 系统结构最好的会议之一。基本上是美国最顶尖的研究小组在上面发表文章,国内的人员很难。系统结构
- ACM/IFIP/USENIX International MiddlewareConference
- ACM MM:ACM Multimedia Conference 领域顶级国际会议,全文的录取率极低,但Poster比较容易。多媒体技术,数据压缩
- MobiSys: The International Conference on Mobile Systems, Applications, and Services 无线方面,2006年第4名。无线
- PLDI: Conference on Programming Language Design and Implementation PLDI是由ACM主办的国际会议,每年一次。主要关注编程语言的设计与实现等方面的研究工作,在国内外学术界很高的影响。
- PODC: Annual ACM Symposium on Principles of Distributed Computing 关注分布式系统的理论,设计,实现,规范等领域的国际会议。近年的接收率在25%左右。
- POPL: Annual Symposium on Principles of Programming Languages 关注programming languages, programming systems, and programming interfaces的design, definition, analysis, and implementation的国际权威会议,始于1973年,接收率不到20%。
- PPoPP: Principles and Practice of Parallel Programming ACM主办的国际会议,两年一次。主要关注并行编程方面的研究,在国内外学术界很高的影响。接收率30%。【2012】
- RTSS- IEEE Real-Time Systems Symposium 实时系统研究的顶级会议,IEEE主办,已经举行了27届。
- SC – IEEE/ACM SC Conference SuperComputing的简称。关注的领域为HPC,networking,storage and analysis。ACM和IEEE合办。【2011】
- SIGGRAPH: ACM SIGGRAPH Conference计算机图形学顶级国际会议,ACM主办,每年一次,几万人参加会议,论文录用率小于20%。计算机图形学
- ACM SIGMETRICS: Conference on Measurement and Modeling of Computer Systems ACM性能建模与评价领域顶级学术会议。通信与网络
- SP:IEEE Security and Privacy
- SPAA:Annual ACM Symposium on Parallel Algorithms and Architectures
- WWW: The ACM International World Wide Web Conference ACM旗下关于互联网方面的重要会议,从Web服务器到互联网语义等研究问题一一包含其中。15%录用率。Internet
三、其他重要会议(TOP80)
- National Conference on Artificial Intelligence (AAAI)
- ACM Conference on Human Factors in Computing Systems (CHI)
- USENIX Large Installation System Administration Conference (LISA)
- IEEE International Conference on Cluster Computing (CLUSTER)【2012】
- Annual International Cryptology Conference (CRYPTO)
- ACM SIGCOMM Internet Measurement Conference (IMC)
- International Symposium on Low Power Electronics and Design (ISLPED)
- IEEE International Magnetics Conference (MC)
- ACM Symposium on the Foundations of Software Engineering (FSE)
- IEEE/ACM International Conference on Grid Computing (GRID)
- Workshop on Hot Topics in Networking (HotNets)
- Workshop on Hot Topics in Operating Systems (HotOS)
- IEEE International Conference on Data Mining (ICDM)
- International Conference on Machine Learning (ICML)
- International Conference on Parallel Processing (ICPP)
- IEEE International ASIC/SOC Conference
- IEEE International Parallel and Distributed Processing Symposium (IPDPS)
- International Semantic Web Conference (ISWC)
- USENIX Linux Kernel Developers Summit (Linux Kernel)
- International Symposium on Modeling, Analysis, and Simulation of Computer & Telecommunication Systems (MASCOTS)
- SPIE Conference on Multimedia Computing and Networking (MMCN)
- International Conference on Mobile Computing and Networking (MobiCom)
- IEEE International Conference on Computer Design (ICCD)
- USENIX Symposium on Networked Systems Design and Implementation (NSDI)【2011】【2012】【2013】
- International Conference on Parallel Architectures and Compilation Techniques (PACT)
- IEEE International Symposium on Information Theory (ISIT)【2012】
- IFIP International Symposium on Computer Performance Modeling, Measurement and Evaluation (Performance)
- SIAM Conference on Parallel Processing for Scientific Computing (PP)
- International Symposium on the Recent Advances in Intrusion Detection (RAID)
- IEEE Real-Time and Embedded Technology and Applications Symposium (RTAS)
- ACM Symposium on Access Control Models and Technologies (SACMAT)【2012】
- USENIX Security Symposium (Security)【2012】【2013】【2014】
- ACM-SIAM Symposium on Discrete Algorithms (SODA)
- International Symposium on Reliable Distributed Systems (SRDS)【2012】
- IEEE Symposium on Mass Storage Systems/NASA Goddard Conference on Mass Storage Systems and Technologies (MSS/MSST)【2013】
- USENIX Symposium on Internet Technologies and Systems (USITS)【没有再开了】
- ACM Conference on Electronic Commerce (EC)
- IEEE International Conference on Communications (ICC)【2013】
- USENIX Workshop on Real, Large Distributed Systems (WORLDS)【没开了】
- IEEE International Symposium on Circuits and Systems (ISCAS)
- Asia-Pacific Computer Systems Architecture Conference (APCSAC)【07 年后就没再开了】
- European Conference on Computer Systems (EuroSys)【2013】
- Workshop on Hot Topics in System Dependability (HotDep)
- Workshop on Hot Topics in Power management (HotPower)
- ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc)
- International Conference on Extending Database Technology (EDBT)
- Workshop on Hot Topics in Storage and File Systems (HotStorage)【2011】【2012】
附上南洋理工大学的Rank(仅列Rank 1):
数据库方向
- SIGMOD: ACM SIGMOD Conf on Management of Data
- PODS: ACM SIGMOD Conf on Principles of DB Systems
- VLDB: Very Large Data Bases
- ICDE: Intl Conf on Data Engineering
- CIKM: Intl. Conf on Information and Knowledge Management
- ICDT: Intl Conf on Database Theory
人工智能和相关方向:
- AAAI: American Association for AI National Conference
- CVPR: IEEE Conf on Comp Vision and Pattern Recognition
- IJCAI: Intl Joint Conf on AI
- ICCV: Intl Conf on Computer Vision
- ICML: Intl Conf on Machine Learning
- KDD: Knowledge Discovery and Data Mining
- KR: Intl Conf on Principles of KR & Reasoning
- NIPS: Neural Information Processing Systems
- UAI: Conference on Uncertainty in AI
- AAMAS: Intl Conf on Autonomous Agents and Multi-Agent Systems (past: ICAA)
- ACL: Annual Meeting of the ACL (Association of Computational Linguistics)
硬件和结构
- ASPLOS: Architectural Support for Prog Lang and OS
- ISCA: ACM/IEEE Symp on Computer Architecture
- ICCAD: Intl Conf on Computer-Aided Design
- DAC: Design Automation Conf
- MICRO: Intl Symp on Microarchitecture
- HPCA: IEEE Symp on High-Perf Comp Architecture
应用和多媒体
- I3DG: ACM-SIGRAPH Interactive 3D Graphics
- SIGGRAPH: ACM SIGGRAPH Conference
- ACM-MM: ACM Multimedia Conference
- DCC: Data Compression Conf
- SIGMETRICS: ACM Conf on Meas. & Modelling of Comp Sys
- SIGIR: ACM SIGIR Conf on Information Retrieval
- PECCS: IFIP Intl Conf on Perf Eval of Comp \& Comm Sys
- WWW: World-Wide Web Conference
系统技术(这个分的有点乱)
- SIGCOMM: ACM Conf on Comm Architectures, Protocols & Apps
- INFOCOM: Annual Joint Conf IEEE Comp & Comm Soc
- SPAA: Symp on Parallel Algms and Architecture
- PODC: ACM Symp on Principles of Distributed Computing
- PPoPP: Principles and Practice of Parallel Programming
- RTSS: Real Time Systems Symp
- SOSP: ACM SIGOPS Symp on OS Principles
- SOSDI: Usenix Symp on OS Design and Implementation
- CCS: ACM Conf on Comp and Communications Security
- IEEE Symposium on Security and Privacy
- MOBICOM: ACM Intl Conf on Mobile Computing and Networking
- USENIX Conf on Internet Tech and Sys
- ICNP: Intl Conf on Network Protocols
- PACT: Intl Conf on Parallel Arch and Compil Tech
- RTAS: IEEE Real-Time and Embedded Technology and Applications Symposium
- ICDCS: IEEE Intl Conf on Distributed Comp Systems
编程语言和软件工程
- POPL: ACM-SIGACT Symp on Principles of Prog Langs
- PLDI: ACM-SIGPLAN Symp on Prog Lang Design & Impl
- OOPSLA: OO Prog Systems, Langs and Applications
- ICFP: Intl Conf on Function Programming
- JICSLP/ICLP/ILPS: (Joint) Intl Conf/Symp on Logic Prog
- ICSE: Intl Conf on Software Engineering
- FSE: ACM Conf on the Foundations of Software Engineering (inc: ESEC-FSE)
- FM/FME: Formal Methods, World Congress/Europe
- CAV: Computer Aided Verification
算法和理论
- STOC: ACM Symp on Theory of Computing
- FOCS: IEEE Symp on Foundations of Computer Science
- COLT: Computational Learning Theory
- LICS: IEEE Symp on Logic in Computer Science
- SCG: ACM Symp on Computational Geometry
- SODA: ACM/SIAM Symp on Discrete Algorithms
- SPAA: ACM Symp on Parallel Algorithms and Architectures
- ISSAC: Intl. Symp on Symbolic and Algebraic Computation
- CRYPTO: Advances in Cryptology